Variedades invariantes de equações diferenciais não-autónomas

Orador: A. J. G. Bento (Departamento de Matemática, UBI). Data, hora e local: 15 de Maio de 2014, início às 15h na sala 6.17.
Resumo: Neste seminário consideraremos a equação diferencial

$\displaystyle v'(t) = A(t)v(t)$ , (1)

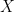
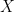
onde $A: [0,+\infty[\rightarrow B(X)$ é uma aplicação contínua, $X$ é um espaço de Banach e $B(X)$ é a algebra dos operadores lineares limitados definidos em $X$ . Supondo que a equação (1) admite um tipo de dicotomia bastante geral, mostraremos que a equação

$v'(t) = A(t)v(t) + f(t, v(t))$ ,

com $f: [0, +\infty[ \times X \rightarrow X$ uma função contínua tal que $f(t, 0) = 0$ , tem uma variedade invariante quando, para cada $t \in [0, +\infty[$ , $f(t,.)$ é Lipschitz ou localmente Lipschitz, com constantes de Lipshitz suficientemente pequenas. Este resultado inclui como casos particulares vários resultados já existentes na literatura. Este seminário está baseado num trabalho conjunto com C.M. Silva.

Seminário realizado com o apoio do Centro de Matemática – 212 (Pest-OE/MAT/UI0212/2014).

Departamento de Matemática

Faculdade de Ciências | Universidade da Beira Interior

Variedades invariantes de equações diferenciais não-autónomas

Deixar uma resposta Cancelar resposta

Related posts

Deixar uma resposta Cancelar resposta